Calculer le rayon d'un verre bombé ou d'un verre cintré

Vous avez besoin d'un mètre et d'une calculatrice.
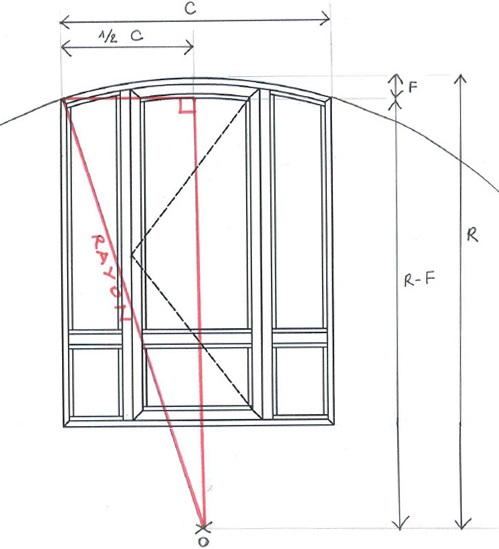
Assurez-vous que le vitrage est bien un arc de cercle (1 seul rayon) et mesurez la corde (la distance entre les 2 extrémités de l'arc) et la flèche (la distance entre la perpendiculaire au milieu de la corde et le sommet de l'arc).
Appliquez ensuite le Théorème de Pythagore.

"Dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des côtés."
Ici, il faut considérer le triangle rectangle matérialisé en rouge sur le croquis. Il est déterminé par les 3 côtés suivants :

le rayon du cercle de centre O (l'hypothénuse) : R
la moitié de la corde : C/2
la différence entre le rayon et la flèche : R-F

Grâce au théorème de Pythagore, savons que :
(R-F)² + (C/2)² = R²
Soit R² - 2RF + F² + (C/2)² - R² = 0
Soit F² + (C/2)² = 2RF
Soit F/2 + C²/8F = R

Source du visuel ou informations : Alco Cintrage